GUIDANCE DOCUMENT
Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials February 2010
Document issued on: February 5, 2010
The draft of this document was issued on 5/23/2006
For questions regarding this document, contact Dr. Greg Campbell (CDRH) at 301-796-5750 or greg.campbell@fda.hhs.gov or the Office of Communication, Outreach and Development, (CBER) at 1-800-835-4709 or 301-827-1800.
 |
U.S. Department of Health and Human Services Division of Biostatistics |
 |
Center for Biologics Evaluation and Research |
Contains Nonbinding Recommendations
Preface
Public Comment
Written comments and suggestions may be submitted at any time for Agency consideration to the Division of Dockets Management, Food and Drug Administration, 5630 Fishers Lane, Room 1061, (HFA-305), Rockville, MD, 20852.
Alternatively, electronic comments may be submitted to http://www.regulations.gov. When submitting comments, please refer to Docket No.2006D-0191. Comments may not be acted upon by the Agency until the document is next revised or updated.
Additional Copies
Additional copies are available from the Internet. You may also send an e-mail request to CDRH-Guidance@fda.hhs.gov to receive a copy of the guidance. Please use the document number 1601 to identify the guidance you are requesting.
Additional copies of this guidance document are also available from the Center for Biologics Evaluation and Research (CBER), Office of Communication, Outreach and Development (HFM-40), 1401 Rockville Pike, Suite 200N, Rockville, MD 20852-1448, or by calling 1-800-835-4709 or 301-827-1800, or email ocod@fda.hhs.gov, or from the Internet at http://www.fda.gov/BiologicsBloodVaccines/ GuidanceComplianceRegulatoryInformation/ Guidances/default.htm
Table of Contents
- Introduction
- Foreword
- 2.1 What is Bayesian statistics?
- 2.2 Why use Bayesian statistics for medical devices?
- 2.3 Why are Bayesian methods more commonly used now?
- 2.4 When should FDA participate in the planning of a Bayesian trial?
- 2.5 The Bayesian approach is not a substitute for sound science.
- 2.6 What are potential benefits of using Bayesian methods?
- 2.7 What are potential challenges using the Bayesian approach?
- 2.8 What software programs are available that can perform Bayesian analyses?
- 2.9 What resources are available to learn more about Bayesian statistics?
- Bayesian Statistics
- 3.1 Outcomes and Parameters
- 3.3 What is a prior distribution?
- 3.4 What is the likelihood of the observed data?
- 3.5 What is the posterior distribution?
- 3.6 What is a predictive distribution?
- 3.7 What is exchangeability?
- 3.8 What is the Likelihood Principle?
- Planning a Bayesian Clinical Trial
- 4.1 Bayesian trials start with a sound clinical trial design
- 4.2 Selecting the relevant endpoints
- 4.3 Collecting other important information: covariates
- 4.4 Choosing a comparison: controls
- 4.5 Initial information about the endpoints: prior distributions
- 4.6 Borrowing strength from other studies: hierarchical models
- 4.7 Determining the sample size
- 4.8 Assessing the operating characteristics of a Bayesian design
- Analyzing a Bayesian Clinical Trial
- 5.1 Summaries of the posterior distribution
- 5.2 Hypothesis testing
- 5.3 Interval estimation
- 5.4 Predictive probabilities
- 5.5 Interim analyses
- 5.6 Model Checking
- 5.7 Sensitivity Analysis
- 5.8 Decision analysis
- Post-Market Surveillance
- Technical Details
- 7.1 Suggested Information to Include in Your Protocol
- 7.2 Simulations to Obtain Operating Characteristics
- 7.3 Model Selection
- 7.4 Checking Exchangeability using the Posterior Predictive Distribution
- 7.5 Calculations
- References
Guidance for Industry and FDA Staff
Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials
| This guidance represents the Food and Drug Administration's (FDA's) current thinking on this topic. It does not create or confer any rights for or on any person and does not operate to bind FDA or the public. You can use an alternative approach if the approach satisfies the requirements of the applicable statutes and regulations. If you want to discuss an alternative approach, contact the FDA staff responsible for implementing this guidance. If you cannot identify the appropriate FDA staff, call the appropriate number listed on the title page of this guidance. |
1. Introduction
This document provides guidance on statistical aspects of the design and analysis of clinical trials for medical devices that use Bayesian statistical methods.
The purpose of this guidance is to discuss important statistical issues in Bayesian clinical trials for medical devices. The purpose is not to describe the content of a medical device submission. Further, while this document provides guidance on many of the statistical issues that arise in Bayesian clinical trials, it is not intended to be all-inclusive. The statistical literature is rich with books and papers on Bayesian theory and methods; a selected bibliography has been included for further discussion of specific topics.
FDA’s guidance documents, including this guidance, do not establish legally enforceable responsibilities. Instead, guidances describe the Agency’s current thinking on a topic and should be viewed only as recommendations, unless specific regulatory or statutory requirements are cited. The use of the word should in Agency guidances means that something is suggested or recommended, but not required.
2. Foreword
2.1 What is Bayesian statistics?
Bayesian statistics is an approach for learning from evidence as it accumulates. In clinical trials, traditional (frequentist) statistical methods may use information from previous studies only at the design stage. Then, at the data analysis stage, the information from these studies is considered as a complement to, but not part of, the formal analysis. In contrast, the Bayesian approach uses Bayes’ Theorem to formally combine prior information with current information on a quantity of interest. The Bayesian idea is to consider the prior information and the trial results as part of a continual data stream, in which inferences are being updated each time new data become available.
Throughout this document we will use the terms “prior distribution”, “prior probabilities”, or simply “prior” to refer to the mathematical entity (the probability distribution) that is used in these Bayesian calculations. The term “prior information” refers to the set of all information that may be used to construct the prior distribution.
2.2 Why use Bayesian statistics for medical devices?
With prior information
When good prior information on clinical use of a device exists, the Bayesian approach may enable this information to be incorporated into the statistical analysis of a trial. In some circumstances, the prior information for a device may be a justification for a smaller-sized or shorter-duration pivotal trial.
Good prior information is often available for medical devices because of their mechanism of action and evolutionary development. The mechanism of action of medical devices is typically physical. As a result, device effects are typically local, not systemic. Local effects can sometimes be predictable from prior information on the previous generations of a device when modifications to the device are minor. Good prior information can also be available from studies of the device overseas. In a randomized controlled trial, prior information on the control can be available from historical control data.
Our experience is that Bayesian methods are usually less controversial when the prior information is based on empirical evidence such as data from clinical trials. However, Bayesian methods can be controversial when the prior information is based mainly on personal opinion (often derived by elicitation from “experts”).
Without prior information
The Bayesian approach is also frequently useful in the absence of prior information. First, the approach can accommodate adaptive trials (e.g., interim analyses, change to sample size, or change to randomization scheme) and even some unplanned, but necessary trial modifications. Second, the Bayesian approach can be useful for analysis of a complex model when a frequentist analysis is difficult to implement or does not exist. Other potential uses include adjustment for missing data, sensitivity analysis, multiple comparisons, and optimal decision making (Bayesian decision theory).
Least burdensome
The Bayesian approach, when correctly employed, may be less burdensome than a frequentist approach.1 Section 513(a)(3) of the Federal Food, Drug, and Cosmetic Act (FFDCA) mandates that FDA shall consider the least burdensome appropriate means of evaluating effectiveness of a device that would have a reasonable likelihood of resulting in approval (see 21 U.S.C. 360c(a)(3)).
2.3 Why are Bayesian methods more commonly used now?
Bayesian analyses are often computationally intense. However, recent breakthroughs in computational algorithms and computing speed have made it possible to carry out calculations for very complex and realistic Bayesian models. These advances have resulted in a huge increase in the popularity of Bayesian methods (cf. Malakoff, 1999). A basic computational tool is a method called Markov Chain Monte Carlo (MCMC) sampling, a method for simulating from the distributions of random quantities.
2.4 When should FDA participate in the planning of a Bayesian trial?
With any clinical trial, we recommend you schedule meetings to discuss experimental design and models. For a Bayesian design we recommend you discuss your prior information with FDA before the study begins. If an investigational device exemption (IDE) is required, we recommend you meet with FDA before you submit the IDE.
2.5 The Bayesian approach is not a substitute for sound science.
Scientifically sound clinical trial planning and rigorous trial conduct are important regardless of whether you use a Bayesian or frequentist approach. We recommend you remain vigilant regarding randomization, concurrent controls, prospective planning, blinding, bias, precision, and all other factors that go into a successful clinical trial. See Section 4.1: Bayesian trials start with a sound clinical trial design.
2.6 What are potential benefits of using Bayesian methods?
2.6.1 More Information for Decision Making
The information from a current trial is augmented and the precision may be increased by the incorporation of prior information in a Bayesian analysis. The Bayesian analysis brings to bear the extra, relevant, prior information, which can help FDA make a decision.
2.6.2 Sample size reduction via prior information
In some instances, the use of prior information may alleviate the need for a larger sized trial.
However, a decrease in the sample size for the current trial may not be warranted by a Bayesian analysis incorporating prior information. See section 4.7 for further discussion on sample size issues in a Bayesian clinical trial.
Additionally, if the prior information does not agree sufficiently with trial results, then the Bayesian analysis may actually be conservative relative to a frequentist or Bayesian analysis that does not incorporate the prior information.
2.6.3 Sample size reduction via Adaptive Trial Design
Adaptive designs use accumulating data to decide on how to modify certain aspects of a trial according to a pre-specified plan. They are often used to potentially reduce the size of a trial by stopping the trial early when conditions warrant. Adaptive trial designs can sometimes be easier to implement using Bayesian methods than frequentist methods. By adhering to the Likelihood Principle, a Bayesian approach can offer flexibility in the design and analysis of adaptive trials (see Sections 3.8 and 4.10).
2.6.4. Midcourse changes to the trial design
With appropriate planning, the Bayesian approach can also offer the flexibility of midcourse changes to a trial. Some possibilities include dropping an unfavorable treatment arm or mo difications to the randomization scheme. Modifications to the randomization scheme are particularly relevant for an ethically sensitive study or when enrollment becomes problematic for a treatment arm. Bayesian methods can be especially flexible in allowing for changes in the treatment to control randomization ratio during the course of the trial. See Kadane (1996) for a discussion.
2.6.5 Other Potential Benefits
Exact analysis
The Bayesian approach can sometimes be used to obtain an exact analysis when the corresponding frequentist analysis is only approximate or is too difficult to implement.
Missing Data
Bayesian methods allow for great flexibility in dealing with missing data. See section 5.4 for a discussion of the use of these Bayesian methods.
Multiplicity
Multiplicity is pervasive in clinical trials. For example, inferences on multiple endpoints or testing of multiple subgroups (e.g., race or sex) are examples of multiplicity. Bayesian approaches to multiplicity problems are different from frequentist ones, and may be advantageous. See section 4.9 for a discussion of Bayesian multiplicity adjustments.
2.7 What are potential challenges using the Bayesian approach?
Extensive preplanning
Planning the design, conduct, and analysis of any trial is always important from a regulatory perspective, but is especially crucial for a Bayesian trial. In a Bayesian trial, decisions have to be made at the design stage regarding:
- the prior information,
- the information to be obtained from the trial, and
- the mathematical model used to combine the two.
Different choices of prior information or different choices of model can produce different decisions. As a result, in the regulatory setting, the design of a Bayesian clinical trial involves pre-specification of and agreement on both the prior information and the model. Since reaching this agreement is often an iterative process, we recommend you meet with FDA early to obtain agreement upon the basic aspects of the Bayesian trial design.2
A change in the prior information or the model at a later stage of the trial may imperil the scientific validity of the trial results. For this reason, formal agreement meetings may be appropriate when using a Bayesian approach. Specifically, the identification of the prior information may be an appropriate topic of an agreement meeting.
Extensive model-building
The Bayesian approach can involve extensive mathematical modeling of a clinical trial, including:
- the probability distributions chosen to reflect the prior information,
- the relationships between multiple sources of prior information,
- the influence of covariates on patient outcomes or missing data, and
- sensitivity analyses on the model choices.
We recommend you make your modeling choices through close collaboration and agreement with FDA and your statistical and clinical experts.
Specific statistical and computational expertise
The Bayesian approach often involves specific statistical expertise in Bayesian analysis and computation. Special computational algorithms like MCMC are often used to
- analyze trial data,
- check model assumptions,
- assess prior probabilities at the design stage,
- perform simulations to assess probabilities of various outcomes, and
- estimate sample size.
The technical and statistical costs involved in successfully designing, conducting, and analyzing a Bayesian trial may be offset by the increased precision on device performance that can be obtained by incorporating prior information, or in the absence thereof, by the benefits of a flexible Bayesian trial design (e.g., smaller expected sample size resulting from interim analysis).
Choices regarding prior information
An FDA advisory panel may question prior information you and FDA agreed upon beforehand. We recommend you be prepared to clinically and statistically justify your choices of prior information. In addition, we recommend that you perform sensitivity analysis to check the robustness of your models to different choices of prior distributions.
Device labeling
Results from a Bayesian trial are expressed differently from the way trial results are usually described in device labels. Bayesian terminology is not yet commonly seen in device labeling3. As always, we recommend you ensure trial results reported on the device label are easy to understand.
Checking calculations
The flexibility of Bayesian models and the complexity of the computational techniques for Bayesian analyses create greater possibility for errors and misunderstandings. As with any submission, FDA will carry out a detailed statistical review, including verifying results using the same or alternate software. FDA recommends you submit your data and any instruction set used by the statistical analysis program in electronic form.
Bayesian and frequentist analyses approaches may differ in their conclusions
Two investigators, each with the same data and a different preplanned analysis (one Bayesian and one frequentist), could conceivably reach different conclusions that are both scientifically valid. While the Bayesian approach can often be favorable to the investigator with good prior information, the approach can also be more conservative than a frequentist approach (e.g., see Section 4: Planning a Bayesian Clinical Trial).
We recommend you do not switch from a frequentist to a Bayesian analysis (or vice versa) once a trial has been initiated. Such post hoc analyses are not scientifically sound and tend to weaken the validity of the submission.
2.8 What software programs are available that can perform Bayesian analyses?
A commonly available, non-commercial software package dedicated to making Bayesian calculations is called WinBUGS4. The acronym BUGS stands for Bayesian Inference Using Gibbs Sampling, a common type of MCMC sampling. WinBUGS has spawned two other software packages, BRUGS and OpenBUGS. BRUGS enables BUGS to be run in the popular non-commercial package R. OpenBUGS is an open source version of BUGS that allows users to modify the programming code in the package. Other Bayesian software packages are likely to become available in the future. We recommend that before you choose a particular software product you consult with FDA statisticians regarding the computations you will be undertaking in your submission.
2.9 What resources are available to learn more about Bayesian statistics?
Non-technical introductory references to Bayesian statistics and their application to medicine include Malakoff (1999), Hively (1996), Kadane (1995), Brophy & Joseph (1995), Lilford & Braunholtz (1996), Lewis & Wears (1993), Bland & Altman (1998), and Goodman (1999a, 1999b). O’Malley & Normand (2003) discuss the FDA process and Bayesian methods for medical device trials. Berry (1997) has written an introduction on Bayesian medical device trials specifically for FDA.
Brophy & Joseph (1995) provide a well-known synthesis of three clinical trials using Bayesian methods. A comprehensive summary on the use of Bayesian methods to design and analyze clinical trials or perform healthcare evaluations appears in Spiegelhalter, Abrams, & Myles (2004).
Introductions to Bayesian statistics that do not emphasize medical applications include Berry (1996), DeGroot (1986), Stern (1998), Lee (1997), Lindley (1985), Gelman, et al. (2004), and Carlin and Louis (2008).
References with technical details and statistical terminology are Spiegelhalter, et al. (2000), Spiegelhalter, et al. (1994), Berry & Stangl (1996), Breslow (1990), Stangl & Berry (1998), and Box and Tiao (1992).
Technical overviews of Markov Chain Monte Carlo methods for Bayesian computation include Gamerman and Lopes (2006) and Chapter 1 of Gilks, Richardson and Spiegelhalter (1996).
Practical applications of Bayesian analyses appear in a number of excellent books, including Spiegelhalter et al (2004),, Congdon (2003), Broemeling (2007), Congdon (2007), Congdon (2005), Albert (2007), and Gilks et al. (1996).
Excellent books on optimal Bayesian decision making (a.k.a., Bayesian decision theory) include Berger (1986), Robert (2007), Raiffa and Schlaifer (2000), a nd MH DeGroot (1970).
A list of resources on the Web appears on the International Society for Bayesian Analysis website.5
3. Bayesian Statistics
3.1 Outcomes and Parameters
Statistics is concerned with making inferences about unknown quantities of interest. A quantity of interest may be:
- an outcome associated with a patient or some other experimental or study unit, or
- a parameter, a quantity that describes a characteristic of the population from which the study is considered to be a sample.
For instance, outcomes in device trials include:
- adverse events (e.g., death, renal failure, bleeding, myocardial infarctions, recurrence),
- measures of effectiveness (e.g., in cardiac function, visual acuity, patient satisfaction), and
- diagnostic test results.
Parameters might describe:
- the rate of serious adverse events,
- the probability of device effectiveness for a patient,
- a patient’s survival probability, and
- sensitivity and specificity of a diagnostic device.
3.2 The Bayesian Paradigm
The Bayesian paradigm states that probability is the only measure of one’s uncertainty about an unknown quantity. In a Bayesian clinical trial, uncertainty about a quantity of interest is described according to probabilities, which are updated as information is gathered from the trial.
Prior distribution
Before a Bayesian trial begins and data are obtained, probabilities are given to all the possible values (or ranges of values) of an unknown quantity of interest. These probabilities, taken together, constitute the prior distribution for that quantity. In trials undergoing regulatory review, the prior distribution is usually based on data from previous trials (although mathematically they need not actually be temporally ordered).
Bayes’ theorem and posterior probabilities
After data from the trial become available, the prior distribution is updated according to Bayes’ theorem. This updated distribution is called the posterior distribution, from which one obtains the probabilities for values of the unknown quantity after data are observed. This approach is a scientifically valid way of combining previous information (the prior probabilities) with current data. The approach can be used in an iterative fashion as knowledge accumulates: today’s posterior probabilities become tomorrow’s prior probabilities.
Bayesian inferences are based on the posterior distribution. For example, a Bayesian decision procedure might rule out a set of parameter values if the posterior probability of the parameter values (given the observed data) is small.
Decision rules
The pre-market evaluation of medical devices aims to demonstrate reasonable assurance of safety and effectiveness of a new device, often through pre-specified decision rules. Traditional hypothesis testing is an example of a type of decision rule. For Bayesian trials, one common type of decision rule considers that a hypothesis has been demonstrated (with reasonable assurance) if its posterior probability is large enough (“large enough” will be discussed later).
The Bayesian approach encompasses a number of key concepts, some of which are not part of the traditional statistical approach. Below, we briefly discuss these concepts and contrast the Bayesian and frequentist approaches.
3.3 What is a prior distribution?
Suppose that the Greek letter θ (“theta”) represents a parameter in a clinical trial. The initial knowledge about θ prior to data collection is represented by the prior distribution for θ, which we denote in symbols as P(θ).
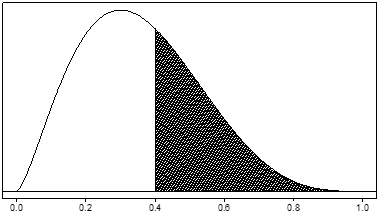
As an example, suppose θ is the rate of a serious adverse event. Its possible values lie between 0 and 1. The prior distribution might give preference to lower values of θ. Figure 1 shows an example of such a prior distribution. The probability that θ takes on any particular set of values is determined by the area under the curve for that set of values. So the prior probability that the adverse event rate θ is greater than 0.4 (the shaded area) is about 0.38.
Figure 1. Example of a unimodal, right-skewed prior dist ribution for a serious adverse event rate, denoted by θ . The prior probability that θ is greater than 0.4 (the shaded area) is about 0.38.
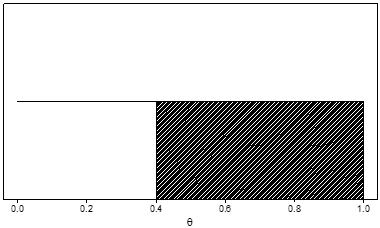
Alternatively, another prior distribution is the uniform distribution indicating no preference for any value of θ. (Figure 2) For a uniform distribution, the probability that θ lies between 0.2 and 0.3 is 0.10, the same as the probability that θ lies between 0.7 and 0.8, or between 0.55 and 0.65, or in any interval of length 0.10. For this prior, the prior probability that θ is greater than 0.4 (again represented by the shaded area) is 0.60.
Figure 2. Example of a uniform prior distribution for a serious adverse event rate, denoted by θ. The prior probability that θ is greater than 0.4 (the shaded area) is 0.60.
3.4 What is the likelihood of the observed data?
Now suppose outcomes have been obtained from a clinical trial. The likelihood function is a mathematical representation of the relationships between observed outcomes and the parameter θ. The likelihood function can be expressed in symbols by P(data |θ), which is the conditional probability of observing the data given a specific value of the parameter θ, for each possible value of θ.
3.5 What is the posterior distribution?
The final objective is to obtain the posterior distribution, the probabilities of the possible values of the parameter θ conditional on the observed data, which can be denoted in symbols as P(θ| data). Bayes’ theorem is used to update the prior distribution for θ, P(θ), via the likelihood, P(data|θ), to obtain the posterior distribution for θ, P(θ|data). The information about θ is summarized by this posterior distribution, and Bayesian inferences are based on it.
As an example, Figure 3 shows the posterior distribution that would be obtained if we started with the prior shown in Figure 1 and observed data with 1 adverse event in 10 patients. Since the adverse event rate observed in these patients is 0.10, the distribution has shifted further to the left (that is, it now favors even lower values for θ). The posterior probability that θ greater than 0.4 (the shaded area) is about 0.04. The probability that the adverse event rate is greater than 0.4 has been reduced from about 0.38 (the prior probability) to about 0.04 (the posterior probability) by the observed trial results.
Figure 3. Example of a unimodal, right-skewed posterior distribution for a serious adverse event rate, denoted by θ, after observing one adverse event in 10 patients and updating the prior probability in Figure 1. The posterior probability that θ is greater than 0.4 (the shaded area) is about 0.04.
The posterior distribution that has been obtained today may serve as a prior distribution when more data are gathered. The more information that is accrued, the less uncertainty there may be about the posterior distribution for θ. As more and more information is collected, the influence of the original prior distribution is usually less. If enough data are collected, the relative importance of the prior distribution will be negligible compared to the likelihood.
3.6 What is a predictive distribution?
The Bayesian approach allows for the derivation of a special type of posterior probability; namely, the probability of unobserved outcomes (future or missing) given what has already been observed. This probability is called the predictive probability. Collectively, the probabilities for all possible values of the unobserved outcome are called the predictive distribution. Predictive distributions have many uses, including:
- determining when to stop a trial (based on predicting outcomes for patients not yet observed),
- helping a physician and patient make decisions by predicting the patient’s clinical outcome, given the observed outcomes of patients in the clinical trial,
- predicting a clinical outcome from an earlier or more easily measured outcome for that patient,
- augmenting trial results for missing data (imputation), and
- model checking.
These uses are discussed in more detail in Section 5. Analyzing a Bayesian Clinical Trial.
3.7 What is exchangeability?
Exchangeability is a fundamental concept underlying statistical inference. It can be of particular importance in Bayesian trials. Formally, we would say that units (patients or trials) are considered exchangeable if the probability of observing any particular set of outcomes on those units is invariant to any re-ordering of the units. This definition can be made clearer through examples.
Exchangeability of patients
In a clinical trial, patients within the trial are usually assumed to be exchangeable. Under exchangeability, patient outcomes are not expected to depend on the order in which the patients were enrolled, the order in which the outcomes are observed, or any other re-indexing or re-numbering of the patients.
If patients in the trial are exchangeable with patients in the population from which they were sampled (e.g., the intended use population), then inferences can be made about the population on the basis of data observed on the trial patients. Thus, the concept of a representative sample can be expressed in terms of exchangeability.
Exchangeability of trials
For a Bayesian clinical trial, another level of exchangeability is often assumed. Namely, the trial can be assumed to be exchangeable with other previous trials when the previous trials are considered to be good prior information. The assumption of trial exchangeability enables the current trial to “borrow strength” from the previous trials, while acknowledging that the trials are not identical in all respects. Thus, exchangeability of trials is important in the development of realistic models for combining trial data with prior information.
Suppose the rate of an adverse event for a device will be estimated in a future Bayesian trial, and several historical trials are proposed as prior information.
All the trials could be considered exchangeable if the adverse event rate for any trial is no more likely to be larger or smaller than that of the other trials. That is, the trial outcomes are not expected to depend on any particular ordering, re-indexing or re-numbering of the trials. In particular, the rate in the future trial is no more likely to be smaller or larger than the rates in the historical trials.
For example, suppose there are two historical trials with adverse event rates of 0.05 and 0.07. Exchangeability of trials is supported if we have no information indicating that the adverse event rate in the future trial will be below, between, or above the two historical trial rates.
Exchangeable trials can be thought of as a representative sample of some super-population of clinical trials. The historical trials then provide information on the super-population, and this information, in turn, provides information on the future trial. In this way, the future trial borrows strength from the historical trials.
Determining exchangeability of trials in practice
From a practical point of view, the judgment regarding exchangeability should have input from the clinical, engineering, and statistical point of view.
- The clinicians should be satisfied that the previous trials that are proposed as prior information are similar enough in design and execution to the current trial. A priori, they should not have any reason to believe that there are systematic differences among the trials in any given direction. In particular, they should not be able to predict the direction of a difference between the proposed trial and any of the other previous trials.
- The engineers should be satisfied that any design or manufacturing differences among the devices in the trials should not alter significantly the expected performance of the devices, at least in terms of the outcome or parameter of interest.
- The statisticians should be able to agree on the appropriate statistical model to be used. The statistical model should be developed in consultation with the clinicians and engineers. In some circumstances, a model can be developed that removes systematic, directional differences among the trials such that exchangeability can still be assumed after adjustment for these differences (see Section 4.6).
Bayesian hierarchical models are used to implement exchangeability of trials and exchangeability of patients within trials (see Section 4: Planning a Bayesian Clinical Trial).
For an introductory discussion of exchangeability, see Gelman et. al. (2004), Spiegelhalter et. al. (2004), or Lad (1996). For technical definitions of exchangeability, see Bernardo & Smith (1995).
3.8 What is the Likelihood Principle?
The Likelihood Principle is an important concept in statistics, but is central to the Bayesian approach. The principle states that all information about the parameter of interest, θ, obtained from a clinical trial, is contained in the likelihood function. In the Bayesian approach, the prior distribution for θ is updated using the information provided by the trial through the likelihood function, and nothing else. Bayesian analysts base all inferences about θ solely on the posterior distribution produced in this manner.
A trial can be altered in many ways without changing the likelihood function. Adherence to the likelihood principle allows for flexibility in conducting Bayesian clinical trials, in particular with respect to:
- modifications to sample size,
- adaptive designs,
- interim looks for the purpose of possibly stopping the trial early, and
- multiplicity.
Note that due to regulatory considerations trial modifications may need to be pre-specified at the design stage.
As outlined above, Bayesian analysts base all inferences on the posterior distribution, which (in adherence to the likelihood principle) is the product only of the prior and the likelihood function. Although the frequentist approach makes extensive use of the likelihood function, frequentist analysis does not always adhere to the likelihood principle. For example, the p-value is based on outcomes that might have occurred but were not actually observed in the trial, that is, on something external to the likelihood.
For more on the Likelihood Principle, see Berger & Wolpert (1988), Berger & Berry (1988), Irony (1993), and Barlow, et al., (1989).
4. Planning a Bayesian Clinical Trial
4.1 Bayesian trials start with a sound clinical trial design
The basic tenets of good trial design are the same for both Bayesian and frequentist trials. Parts of a comprehensive trial protocol include:
- objectives of the trial,
- endpoints to be evaluated,
- conditions under which the trial will be conducted,
- population that will be investigated, and
- planned statistical analysis.
We recommend you follow the principles of good clinical trial design and execution, including minimizing bias. Randomization minimizes bias that can be introduced in the selection of which patients get which treatment. Randomization allows concrete statements about the probability of imbalances in covariates due to chance alone. For reasonably large sample sizes, randomization ensures some degree of balance for all covariates, including those not measured in the study.
Masking (also known as blinding) of physicians avoids bias that can be introduced by intended or unintended differences in patient care or in evaluation of patient outcomes based on the treatment received during the course of the trial. Masking of patients minimizes biases due to their expectation of benefit.
We recommend you choose beforehand the type of analysis to be used (Bayesian or frequentist). Switching to an analysis method that produces a more favorable outcome after observing the data is problematic. It is difficult to justify such a switch at the analysis stage. In some cases, a Bayesian analysis of a new trial may salvage some information obtained in a previous non-Bayesian clinical trial that deviated from the original protocol. The information provided by such a trial may be represented by a prior distribution to be used in a prospective Bayesian clinical trial.
For further information on planning a trial, see FDA’s Statistical Guidance for Non-Diagnostic Medical Devices.6
4.2 Selecting the relevant endpoints
Endpoints (also called parameters in this document) are the measures of safety and effectiveness used to support a certain claim. Ideally, endpoints are:
- clinically relevant,
- directly observable,
- related to the claims for the device, and
- important to the patient.
For example, an endpoint may be a measure of the average change in an important outcome (mortality, morbidity, quality of life) observed in the trial.
The objective of a clinical trial is to gather information from the patients in the trial to make inferences about these unknown endpoints or parameters.
4.3 Collecting other important information: covariates
Covariates, also known as confounding factors, are characteristics of the study patients that can affect their outcome. There are many statistical techniques (Bayesian and frequentist) to adjust for covariates. Covariate adjustment is especially important in any situation where some degree of covariate balance is not assured through randomization, such as a Bayesian trial in which other trials are used as prior information. If adjustments are not made for differences in the covariates between trials, the analysis can be biased. Covariate adjustment is also often used to reduce variation, which leads to a more powerful analysis.
4.4 Choosing a comparison: controls
To facilitate evaluation of clinical trial results, we recommend you use a comparator, or control group, as a reference. Types of control groups that may be considered are:
- concurrent controls,
- self controls, and
- historical controls.
We believe that self controls and historical controls have more potential for bias than concurrent controls because of:
- potential problems with covariate adjustment,
- placebo effect, and
- regression to the mean.
Another way to characterize the type of control is to distinguish between controls that are treated with an effective therapy (active controls) vs. controls that either receive no treatment (inactive controls) or are treated with a sham device (placebo controls). Bayesian methods are especially useful with active controlled trials seeking to demonstrate a new device is not only non-inferior to the active control but is also superior to no treatment or a sham control. A Bayesian trial can investigate this question by using previous studies comparing the active control to the inactive control. Bayesian methods for active control trials are discussed in Gould (1991) and Simon (1999).
Bayesian methods can be useful for combining historical controls with concurrent controls. The historical controls act as prior information for the concurrent control. Bayesian methods for utilizing historical controls as prior information are discussed in Pocock (1976) and in Spiegelhalter et al. (2004).), and O’Malley, Normand, and Kuntz (2003), who apply their methods to historical controls for coronary artery stent trials.
4.5 Initial information about the endpoints: prior distributions
Recall that the state of our knowledge (or lack thereof) regarding a quantity of interest before we carry out a study is described by the priordistribution. Appropriate prior information should be carefully selected and incorporated into the analysis correctly. Discussions with FDA regarding study design will include an evaluation of the model to be used to incorporate the prior information into the analysis.
Choosing sources of prior information
We recommend you identify as many sources of good prior information as possible. The evaluation of “goodness” of the prior information is subjective. Because your trial will be conducted with the goal of FDA approval of a medical device, you should present and discuss your choice of prior information with FDA reviewers (clinical, engineering, and statistical) before your study begins.
Possible sources of prior information include:
- clinical trials conducted overseas,
- patient registries,
- clinical data on very similar products, and
- pilot studies.
When an Investigational Device Exemption (IDE) is required, you must submit a complete report of prior investigations.7 In addition to this report, we recommend that you also submit any additional information you propose to use in your analysis that constitutes prior information. In some cases, otherwise valid prior information may be unavailable (e.g., the data may belong to someone else who is unwilling to allow legal access). We recommend you hold a pre-IDE meeting with FDA to come to agreement on what prior information will be used and how it will be used in the analysis.
Prior distributions based directly on data from other studies are the easiest to evaluate. While we recognize that two studies are never exactly alike, we nonetheless recommend the studies used to construct the prior be similar to the current study in the following aspects:
- protocol (endpoints, target population, etc.), and
- time frame of the data collection (e.g., to ensure that the practice of medicine and the study populations are comparable)
In some circumstances, it may be helpful if the studies are also similar in investigators and sites.
Include studies that are favorable and non-favorable. Including only favorable studies creates bias. Bias, based on study selection may be evaluated by:
- the representativeness of the studies that are included, and
- the reasons for including or excluding each study.
Prior distributions based on expert opinion rather than data can be problematic. Approval of a device could be delayed or jeopardized if FDA advisory panel members or other clinical evaluators do not agree with the opinions used to generate the prior.
Informative and non-informative prior distributions
An informative prior distribution gives preferences to some values of the quantity of interest as being more likely than others (such as Figure 1). These preferences are usually based on previous studies. Lack of preference among the values or lack of information can be represented through a non-informative prior distribution (such as Figure 2).
Incorporating informative prior distributions
A Bayesian analysis of a current study of a new device may include prior information from:
- the new device,
- the control device, or
- both devices.
When incorporating prior information from a previous study, the patients in the previous study are rarely considered exchangeable with the patients in the current study. Instead, a hierarchical model is often used to “borrow strength” from the previous studies. At the first level of the hierarchy, these models assume that patients are exchangeable within a study but not across studies. At a second level of the hierarchy, the previous studies are assumed to be exchangeable with the current study, which acknowledges variation between studies. For more detail on hierarchical models, see Section 4.6.
If the prior information for a study is based on many more patients than are to be enrolled in the study, the prior distribution may be too informative. The judgment of what constitutes too informative is a case-by-case decision. In this case, some modifications to the study design and analysis plan may be warranted.
Non-informative prior distributions
Non-informative prior distributions are used frequently in Bayesian adaptive trials when no prior information is available. As another example, in a Bayesian hierarchical model for combining studies, a non-informative prior distribution may be placed on a parameter that captures the variability between studies because, ordinarily, no informative prior is available on this parameter.
There is broad literature on the issues surrounding prior distributions, for example the definition of “non-informative”, the effect of changes in the measurement scale, et cetera. Discussion of these issues can be found in Lee (1997), Kass & Wasserman (1996), Box & Tiao (1973), Bernardo & Smith (1993), and Bernardo, Berger, and Sun (2008). Irony & Pennello (2001) discuss prior distributions for trials under regulatory review.
4.6 Borrowing strength from other studies: hierarchical models
Bayesian hierarchical modeling is a specific methodology you may use to combine results from multiple studies to obtain estimates of safety and effectiveness parameters. The name hierarchical model derives from the hierarchical manner in which observations and parameters are structured. Some Bayesian analysts refer to this approach as “borrowing strength.” For device trials, the amount of strength borrowed can be translated into sample size, and the extent of borrowing depends on how closely results from the current study (the study of interest) reflect the results from the previous studies (from whence we are “borrowing strength”; note that mathematically these need not necessarily occur at an earlier point in time).
If results are very similar, the current study can borrow considerable strength. As current results vary from the previous information, the current study borrows less and less. Very different results borrow no strength at all, or even potentially “borrow negatively”. In a regulatory setting, hierarchical models can be very appealing: They reward having good prior information on device performance by lessening the burden in demonstrating safety and effectiveness. At the same time, the approach can protect against over-reliance on previous studies that turn out to be overly optimistic for the pivotal study parameter.
An example of a hierarchical model
Suppose you want to combine information on the success probabilities from two earlier studies of an approved device with results from a new study. You may decide to use two levels in a hierarchical model: the patient level and the study level.
The first (patient) level of the hierarchy assumes that within each study (current or historical), patients are exchangeable. However, patients from previous studies are not exchangeable with patients in the current study, so patient data from the earlier studies and the current study may not be simply pooled.
The second (study) level of the hierarchy applies a model that assumes the success probabilities from the previous studies and the current study are exchangeable, but the success probabilities may differ. This assumption is prudent since you are not sure if patients from the previous studies are directly exchangeable with the patients from the current study. However, the success probabilities from all three studies are related in that they are assumed exchangeable. As a result, the previous studies provide some information about the success probability in the current study, although not as much information as if the patients in the three groups were directly poolable.
Similarity of previous studies to the current study
The key clinical question in using hierarchical modeling to borrow strength from previous studies is whether the previous studies are sufficiently similar to the current study to be considered exchangeable, as discussed in Section 3.7.
To achieve study exchangeability, statistical adjustments for certain differences in covariates such as demographic and prognostic variables using patient-level data may be necessary. This is called exchangeability conditioned on covariates. Generally, proper calibration of your study depends on having the same covariate information at the patient level as in previous studies, and on incorporating it appropriately. For example, if prior information from historical controls is to be used to augment the sample size in a concurrent control group, but covariates indicate that the concurrent control patients are healthier, then exchangeability of the historical and concurrent controls may be plausible only after adjustment for the covariates (Pennello and Thompson, 2008, Section 3; O’Malley, Normand, and Kuntz, 2003).
Calibration based only on covariate summaries (such as from the literature) may be inadequate because the relationship of the covariate level to the outcome can be determined in the current study but not in the previous studies. This forces the untestable assumption that covariate effects in your study and in the previous studies are the same; that is, that study and covariate effects do not interact.
Previous studies with large sample sizes in a hierarchical model can be very informative. As we will discuss in Section 7.1, if the prior probability of a successful trial is too high, it might be necessary to modify the study design and analysis plan.
Hierarchical models may also be used to combine data across centers in a multi-center trial. For an example, see the Summary of Safety and Effectiveness for PMA P980048, BAK/Cervical Interbody Fusion System by Sulzer Spine-Tech.8
Outcomes for devices can vary substantially by site due to such differences as:
- physician training,
- technique,
- experience with the device,
- patient management, and
- patient population.
A hierarchical model on centers assumes that the parameter of interest varies from center to center but that center-specific parameters are related via exchangeability. This kind of model adjusts for center-to-center variability when estimating the parameter over all centers.
Introductory discussion of hierarchical models and technical details on their implementation appear in Gelman et al. (2004). Other, more complex approaches are described in Ibrahim & Chen (2000) and Dey et al. (1998).
4.7 Determining the sample size
The sample size in a clinical trial depends on:
- variability of the sample,
- prior information,
- mathematical model used in analysis,
- distributions of parameters in the analytic model, and
- specific decision criteria.
If the outcomes are highly variable, the required sample size can be large. If there is no variability (i.e., everyone in the population has the same value for the outcome of interest), a single observation may be sufficient. The purpose of sizing a trial is to gather enough information to make a decision while not wasting resources or putting patients at unnecessary risk.
In traditional frequentist clinical trial design, the sample size is determined in advance. As an alternative to specifying a fixed sample size, the Bayesian approach (and some modern frequentist methods) may specify a particular criterion to stop the trial. Appropriate stopping criteria may be based on a specific amount of information about the parameter (e.g., a sufficiently narrow credible interval, defined in Section 5: Analyzing a Bayesian Clinical Trial) or an appropriately high probability for a pre-specified hypothesis.
At any point before or during a Bayesian clinical trial, you can obtain the predictive distribution for the sample size. Therefore, at any point in the trial, you can compute the expected additional number of observations needed to meet the stopping criterion. In other words, the predictive distribution for the sample size is continuously updated as the trial goes on. Because the sample size is not explicitly part of the stopping criterion, the trial can be ended at the precise point where enough information has been gathered to answer the important questions.
Special considerations when sizing a Bayesian trial
When sizing a Bayesian trial, FDA recommends you decide in advance the minimum sample size according to safety and effectiveness endpoints because safety endpoints may produce a larger sample size. FDA also recommends you include a minimum level of information from the current trial to enable verification of model assumptions and appropriateness of prior information used. This practice also enables the clinical community to gain experience with the device.
When hierarchical models are used, we also recommend you provide a minimum sample size for determining the amount of information that will be “borrowed” from other studies.
We recommend the maximum sample size be defined according to economical, ethical, and regulatory considerations.
Various approaches to sizing a Bayesian trial are described in Inoue et al. (2005), Katsis & Toman (1999), Rubin & Stern (1998), Lindley (1997), and Joseph et al. (1995a,b).
4.8 Assessing the operating characteristics of a Bayesian design
Because of the inherent flexibility in the design of a Bayesian clinical trial, a thorough evaluation of the operating characteristics should be part of the trial planning. This includes evaluation of:
- probability of erroneously approving an ineffective or unsafe device (type I error rate),
- probability of erroneously disapproving a safe and effective device (type II error rate),
- power (the converse of type II error rate: the probability of appropriately approving a safe and effective device),
- sample size distribution (and expected sample size),
- prior probability of claims for the device, and
- if applicable, probability of stopping at each interim look.
A more thorough discussion appears in Technical Details, Section 7.
“Pure” Bayesian approaches to statistics do not necessarily place the same emphasis on the notion of control of type I error as traditional frequentist approaches. There have, however, been some proposals in the literature that Bayesian methods should be “calibrated” to have good frequentist properties (e.g. Rubin, 1984; Box, 1980). In this spirit, as well as in adherence to regulatory practice, FDA recommends you provide the type I and II error rates of your proposed Bayesian analysis plan (see Technical Details, Section 7).
For Bayesian trials, here are some points to consider regarding type I error:
- FDA considers type I error, along with other operating characteristics of the trial design, in evaluating submissions. We strive for reasonable control of the type I error rate. An adequate characterization of the operating characteristics of any particular trial design may need extensive simulations. For more discussion, see Section 7.4, Technical Details.
- When using prior information, it may be appropriate to control type I error at a less stringent level than when no prior information is used. For example, if the prior information is favorable, the current trial may not need to provide as much information regarding safety and effectiveness. The degree to which we might relax the type I error control is a case-by-case decision that depends on many factors, primarily the confidence we have in the prior information.
- We may recommend discounting of historical/prior information if the prior distribution is too informative relative to the current study. What constitutes “too informative” is also a case-by-case decision.
4.9 Bayesian Multiplicity Adjustments
Multiplicity within a clinical trial can be an important regulatory concern because the Agency is concerned with making incorrect decisions; multiplicity can inflate the probability of an incorrect decision of approval.
Multiplicity can greatly affect the statistical interpretation of a clinical trial. For example, if 20 independent subgroups of a frequentist trial are each tested for a significant device effect at Type I error level 5%, then the chance of at least one falsely significant result can be as high as 64%. The typical frequentist approach is to lower the error levels of the individual tests such that the overall chance of a falsely significant result is controlled at a reasonable level, say 5%. However, this approach also lowers the chance of detecting real effects (i.e., power), often substantially. Equivalently, the chance of not detecting a real effect (i.e., a Type II error) increases.
Instead, a possible Bayesian approach to the subgroup problem mentioned above is to consider the subgroups as exchangeable, a priori, through the use of a hierarchical model. This modeling makes the Bayesian estimate of the device effect for a subgroup “borrow strength” from the other subgroups. If the observed device effect for a subgroup is large, then the Bayesian estimate is adjusted according to how well the other subgroups either support or cast doubt on this observation. For more discussion see Dixon and Simon (1991) and Pennello and Thompson (2008).
Bayesian adjustments to multiplicity can be acceptable to FDA, provided the the analysis plan has been pre-specified and the operating characteristics of the analysis are adequate (see Section 4.8). Please consult FDA early on with regard to a statistical analysis plan that includes Bayesian adjustment for multiplicity.
Selected references on Bayesian adjustments for multiplicity are Scott and Berger (2006), Duncan and Dixon (1983), Berry (1988), Gonen et. al. (2003), Pennello (1997), and Lewis and Thayer (2004).
4.10 Bayesian Adaptive Designs
Introduction
Adaptive designs use accumulating data to decide on how to modify certain aspects of a trial according to a pre-specified plan without undermining the validity and integrity of the trial. Adaptive trial designs have the potential to provide optimal statistical inference and to improve quality, speed and efficiency of decision making.
The Likelihood Principle, inherent to the Bayesian approach, makes adaptive designs and interim analyses natural. An adaptive Bayesian clinical trial can involve:
- Interim looks to adapt sample size (to stop or to continue patient accrual)
- Interim looks for the purpose of possibly stopping the trial early either for success, futility, or harm
- Switching the hypothesis of non-inferiority to superiority or vice-versa
- Dropping arms or doses
- Adaptive randomization, i.e., modification of the randomization rate during a trial to increase the probability that a patient be allocated to the best treatment
Efficient Decision Making
A trial design that is adaptive to information as it is accrued can allow for a decision to be made in an efficient way. According to the Bayesian approach, information from a trial should be gathered until it is deemed sufficient for a decision to be made. However, before the trial starts, there is a great deal of uncertainty on the sample size that will provide enough information for a decision to be made. If the variability of the sample is larger than expected, a larger sample size will be needed whereas if the variability is smaller than expected, a smaller sample size will suffice. When adaptive designs are used, the variability of the sample is learned as the trial takes place and less information will be lacking or wasted.
As an example, consider active-controlled (non-inferiority) trials where the endpoint is the device success rate. Here, the sample size depends critically on the control and treatment success rates. For example, consider a situation with a non-inferiority margin of 0.10. Suppose the true control and treatment success rates are both 0.60 and the required sample size is 300 patients per group. If the success rate for the treatment group is 0.65 rather than 0.60 then the sample size will be reduced to approximately 130 patients per group. It is clear that it would be desirable to adapt between these two scenarios since the savings in sample size could be considerable.
Regulatory Considerations
The Agency recognizes that a purely Bayesian approach would allow for continuous design adaptation as the trial take place. However, for regulatory purposes and in order to maintain the integrity of the trial while minimizing operational biases, we strongly recommend that an adaptive trial be planned in advance and that the operating characteristics of the design be assessed in a variety of scenarios at the IDE stage (see 4.8). In other words, the Bayesian adaptive trial should be adaptive by design.
Practical Implementation
Implementation of adaptive designs may be challenging because the confidentiality of the data needs to be maintained to avoid operational biases, that is, investigator bias, selection bias, and patient bias. For instance, if the investigator knows that one treatment is doing better at an interim analysis, he or she may assign it with a higher probability to future patients. In order to minimize operational biases, the design should be well planned in advance and the adaptive algorithm should be pre-specified. Third party analyses and firewalls are recommended. When blinding is essential to assure unbiasedness, the details of the adaptive design that may reveal evolving treatment differences may be best referred to Institutional Review Boards (IRBs) to avoid unblinding issues.
Enrollment rates greatly impact adaptive trials. When enrollment rates are too high vis-à-vis the length of follow-up, adaptations may not be possible because by the time interim results are available, all patients may be already enrolled. As a consequence, the sponsor should be able to control enrollment rates in order to benefit from adaptive designs. In addition, the benefits of fast enrollment should be weighed against benefits of slower controlled enrollment before decisions on adaptive designs are made.
5. Analyzing a Bayesian Clinical Trial
5.1 Summaries of the posterior distribution
Recall that the posterior distribution contains all information from the prior distribution, combined with the results from the trial via the likelihood function. Conclusions from a Bayesian trial are based only on the posterior distribution. FDA recommends you summarize the posterior distribution with a few numbers (e.g., posterior mean, standard deviation, credible interval), especially when there are numerous endpoints to consider. FDA also recommends you include graphic representations of the appropriate distributions.
5.2 Hypothesis testing
Statistical inference may include hypothesis testing, interval estimation, or both. For Bayesian hypothesis testing, you may use the posterior distribution to calculate the probability that a particular hypothesis is true, given the observed data.
5.3 Interval estimation
Bayesian interval estimates are based on the posterior distribution and are called credible intervals. If the posterior probability that an endpoint lies in an interval is 0.95, then this interval is called a 95 percent credible interval. FDA strongly encourages reporting of credible intervals for Bayesian trials in the labeling. For an example on how credible intervals are reported, see the Summary of Safety and Effectiveness for InFuse Bone Graft / LT-CAGE ™ 9 .
Two types of credible intervals are highest posterior density (HPD) intervals (Lee, 1997) and central posterior intervals. For construction of credible intervals, see Chen & Shao (1999) and Irony (1992).
5.4 Predictive probabilities
Uses of predictive probabilities (Section 3.6) include the following:
Deciding when to stop a trial
If it is part of the clinical trial plan, you may use a predictive probability at an interim point as the rule for stopping your trial. If the predictive probability that the trial will be successful is sufficiently high (based on results at the interim point), you may be able to stop the trial and declare success. If the predictive probability that the trial will be successful is small, you may stop the trial for futility and cut losses.
Exchangeability is a key issue here; these predictions are reasonable only if you can assume the patients who have not been observed are exchangeable with the patients who have. This assumption is difficult to formally evaluate but may be more plausible in some instances (e.g., administrative censoring) than others (e.g., high patient drop-out).
Predicting outcomes for future patients
You may also calculate the predictive probability of the outcome of a future patient, given the observed outcomes of the patients in a clinical trial, provided the current patient is exchangeable with the patients in the trial. In fact, that probability answers the following questions:
- Given the results of the clinical trial, what is the probability that a new patient receiving the experimental treatment will be successful?
- What would that probability be if the patient were treated in the control group?
We recommend that you consider the usefulness of this information in helping physicians and patients make decisions regarding treatment options and whether it should be included in the device labeling.
Predicting (imputing) missing data
You may use predictive probabilities to predict (or impute) missing data, and trial results can be adjusted accordingly. There are also frequentist methods for missing data imputation.
Regardless of the method, the adjustment depends on the assumption that patients with missing outcomes follow the same statistical model as patients with observed outcomes. This means the missing patients are exchangeable with the non-missing patients, or that data are missing at random. If this assumption is questionable, FDA recommends you conduct a sensitivity analysis using the prediction model. For examples of missing data adjustments and sensitivity analysis, see the Summary and Safety Effectiveness for PMA P980048, BAK/Cervical Interbody Fusion System, by Sulzer Spine-Tech.10
When the missing data are suspected not to be missing at random, a sensitivity analysis can be built into the computational code to determine what degree of departure from the missing at random assumption is needed for conclusions to change (reference cf. Sulzer-Spine PMA SSED), which can help in alleviating the concern that the missing data may lead to invalid conclusions.
Predicting a clinical outcome from earlier measurements
If patients have measurements of the same outcome at earlier and later follow-up visits, you may make predictions for the later follow-up visit (even before the follow-up time has elapsed). Basing predictions on measures at the earlier visit requires that:
- some patients have results from both follow-up visits
- there is sufficiently high correlation between the early and the later measurement.
In this example, the outcome at the first time point is being used to predict the outcome at the second. This type of prediction was used to justify early stopping for the clinical trial of the INTERFIX Intervertebral Body Fusion Device.11
The earlier measurement may also be on a different outcome; for example, for breast implants, rupture may be predictive of an adverse health outcome later.
5.5 Interim analyses
FDA recommends you specify your method for analyzing interim results in the trial design and ensure FDA agrees in advance of the trial. The following describes two specific Bayesian interim analysis methods:
Applying posterior probability
One method stops the trial early if the posterior probability of a hypothesis at the interim look is large enough. In other words, the same Bayesian hypothesis test is repeated during the course of the trial.
Applying predictive distribution
As mentioned in Section 5.4, another method calculates at interim stages the probability that the hypothesis test will be successful. This method uses the Bayesian predictive distribution for patients yet to be measured. If the predictive probability of success is sufficiently high, the trial may stop early. If the predictive probability is very low, the trial may stop early for futility. This method was used in the submission of the INTERFIX Intervertebral Body Fusion Device.12
5.6 Model Checking
Model checking
FDA recommends you investigate all assumptions important to your analysis. For example, an analysis of a contraceptive device might assume the monthly pregnancy rate is constant across the first year of use. To assess this assumption, the observed month-specific rates may be compared to their predictive distribution. You may summarize this comparison using a Bayesian p-value (Gelman et al., 1996, 2004), the predictive probability that a statistic is equal to or more extreme than that observed under the assumptions of the model. You may also assess model checking and fit by Bayesian deviance measures, such as the Deviance Information Criterion as described in Spiegelhalter et al. (2002). Alternatively, two models may be compared using Bayes factors. More discussion of these assessments is given in Technical Details (Section 7.2).
For example, patients enrolled later in a trial may have a different success rate with the device than those enrolled earlier if:
- physicians have to overcome a learning curve in using the device,
- physicians form an opinion on whom the device treats best, and then enroll more or less favorable patients in the trial,
- an effective adjunctive therapy becomes available to the patients in the trial, or
- an alternative treatment becomes available during the course of the trial, potentially altering the characteristics of the patients who choose to enroll in the trial.
In principle, the assumption that the patients earlier in the trial are exchangeable with patients later in the trial can be checked using any of the methods suggested above.
5.7 Sensitivity Analysis
Sensitivity analysis is used to investigate the effects of deviations from your statistical model and its assumptions. FDA may recommend that you submit a sensitivity analysis. This might include investigations of:
- deviations from the distributional assumptions (i.e. deviations from the assumptions regarding the stochastic elements of your model),
- alternative functional forms for the relationships in your model,
- alternative prior distributions,
- alternative “hyperprior” parameters in hierarchical models, or
- deviations from any “missing at random” assumptions for missing data.
5.8 Decision analysis
Decision analysis is a prescriptive approach that enables a decision maker to logically analyze a problem in order to choose the best course of experimentation and action in the presence of uncertainty.
A decision analysis method considers the consequences of decisions and experimentation to obtain optimum courses of action. Courses of action might include decisions to stop or continue a study or to approve or not approve a medical device.
In any regulatory review of trial results, the consequences of possible decisions should be evaluated and reflected in the values of the posterior probabilities that will be used in order to make the claims. The more critical the endpoint, the more information about that endpoint will be necessary, and the sharper should be its posterior distribution. For example, if there is a possibility of death or serious disability with the use of the device, the Agency will want to be sure that the chance of occurrence of such event is small. A reasonable degree of certainty could be 90%, 95% or even 99%. These values will be reflected in the pre-specified posterior probabilities that the endpoints are below a certain target, or that the difference between the chances of death when using the new device and the control is smaller than a pre-specified value.
A decision analysis method might in principle be used to develop an interim analysis plan. Carlin, Kadane, & Gelfand (1998) propose a method to approximate a decision analysis approach in interim analyses.
For an excellent insight on the decision analysis approach to inference and hypothesis testing see Lee (1997), Chapter 7. More advanced texts on the topic are, in order of complexity, Raiffa (1968), Lindley (1984), Bernardo and Smith (1993), Raiffa and Schlaiffer (1961), Berger (1985), DeGroot (1970), Ferguson (1967).
6. Post-Market Surveillance
FDA believes the Bayesian approach is well suited for surveillance purposes. The key concept: “Today’s posterior is tomorrow’s prior” allows you to use the posterior distribution from a pre-market study as a prior distribution for surveillance purposes, to the extent that data from the clinical study reflect how the device is used after approval. In other words, you may readily update information provided by a pre-market clinical trial with post-market data via Bayes’ theorem if you can justify exchangeability between pre- and post-market data. You may continue to update post-market information via Bayes’ theorem as more data are gathered.
You may also use Bayesian models to mine large databases of post-market medical reports. DuMouchel (1999) discusses Bayesian models for analyzing a very large frequency table that cross-classifies adverse events by type of drug used. DuMouchel uses a hierarchical model to smooth estimates of relative frequencies of adverse events associated with drugs to reduce the number of falsely significant associations that are expected due to multiplicity. It is unclear at this time if this approach is as useful for medical device reports as it is with drug reports.
7. Technical Details
7.1 Suggested Information to Include in Your Protocol
In addition to the standard clinical trial protocol, FDA believes there are statistical issues unique to Bayesian trial designs that should be addressed in your submission. The following suggestions (not an exhaustive listing) will facilitate a smoother review process and serve as a starting point when writing your protocol. Not all points apply to all studies.
Prior information
FDA recommends you indicate all prior information you will use and the assumptions you are making.
Criterion for success
FDA recommends you provide a criterion for success of your study (related to safety and effectiveness).
Justification for the proposed sample size
FDA also recommends you justify your proposed sample size. The method of justification may differ, depending on the trial design.
For example, in a fixed-sample-sized trial, you might choose to simulate data assuming a range of different true parameter values and different sample sizes. For each simulated data set, we recommend you determine the posterior distribution of the parameter. The posterior distribution can be used to compute a credible interval or the posterior probability of the study claim, for example. For each simulation, the credible interval or posterior probability is compared with the “true” parameter value known in the simulation. Repeated simulations are used to assess the proposed sample size. This approach to sample size calculation, can involve intensive simulation. For some situations, simpler methods can be appropriate to obtain an approximation to the sample size. Pennello and Thompson (2008, Section 2) review some of these methods.
For an adaptive trial design, the sample size is a function of the study design parameters and the results of the trial (for example the maximal sample size, the spacing and timing of interim looks, the criteria for stopping the trial). Before the trial begins we recommend you provide the minimum and maximum sample sizes, the number of interim analyses, and the number of patients at each interim analysis.
Operating characteristics (power and type I error rate)
FDA recommends you provide tables of the probability of satisfying the study claim, given various “true” parameter values (e.g., event rates) and various sample sizes for the new trial. This table will also provide an estimate of the probability of a type I error in the case where the true parameter values are consistent with the null hypothesis, or power in the case where the true parameter values are consistent with the alternative (see section 4.8 for definitions).
In some simple cases (e.g. a single arm trial with a binomial outcome) these probabilities can be calculated directly. If the study design is complex it is usually necessary to use simulation to compute these probabilities. In general, the simulation should reflect the study design. Some suggestions on simulation are outlined in Technical Details 7.2:Simulations to Obtain Operating Characteristics.
Prior probability of the study claim
FDA recommends you evaluate the prior probability of your study claim if you are using an informative prior distribution. This is the probability of the study claim before seeing any new data, and it should not be too high. What constitutes “too high” is a case-by-case decision. In particular, we recommend the prior probability not be as high as the success criterion for the posterior probability.
FDA makes this recommendation to ensure the prior information does not overwhelm the current data, potentially creating a situation where unfavorable results from the proposed study get masked by a favorable prior distribution. In an evaluation of the prior probability of the claim, FDA will balance the informativeness of the prior against the gain in efficiency from using prior information as opposed to using noninformative priors.
To calculate this prior probability, you can simulate data using only the prior distribution. For example, if you are using a computer program that performs Markov Chain Monte Carlo (MCMC) simulation, you provide no current data and have the program simulate these values instead. Simulations done in this manner provide the prior probability of the study claim.
If necessary, the prior probability of the study claim can be lowered by modifying the prior distribution on the variance among studies to have a larger prior mean than initially. Alternatively, the prior distribution of the variance can be restricted to be greater than a constant, and the constant can be varied until the prior probability of the claim is lowered to the desired value. These approaches can work for three or more studies. However, for only two studies, i.e., a proposed and a previous study, the prior distribution may also have to be fairly precise because data from two studies may not by themselves provide much information about this variance.
Effective Sample Size
A useful summary that can be computed for any simulations using posterior variance information is the effective sample size in the new trial. That is,
Effective sample size (ESS) is given by:
ESS = n * V1/V2,
Where n = the sample size in the new trial
V1 = the variance of the parameter of interest without borrowing (computed using a non-informative prior distribution)
V2 = the variance of the parameter of interest with borrowing (computed using the proposed informative prior)
Then, the quantity (ESS – n) can be interpreted as the number of patients “borrowed” from the previous trial. This summary is useful in quantifying the efficiency you are gaining from using the prior information. It is also useful for gauging if the prior is too informative. For example, if the number of patients “borrowed” is larger than the sample size for the trial, then the prior may be too informative and may need to be modified by using, for example, the techniques mentioned above (see last paragraph of previous subsection).
Program code
FDA recommends you submit the program code and any data that you use to conduct simulations as part of the IDE submission. We also recommend you include an electronic copy of the data from the study and the computer code used in the analysis with the PMA submission13. (Note we do NOT want the actual software products; instead we are requesting the instruction set that directs how the software performs your analyses.)
7.2 Simulations to Obtain Operating Characteristics
FDA usually recommends you provide simulations of your trial at the planning (or IDE) stage. This will facilitate FDA’s assessment of the operating characteristics of the Bayesian trial; specifically, the type I and type II error rates. We recommend your simulated trials mimic the proposed trial by considering the same:
- prior information,
- sample size,
- interim analyses, and
- possible modifications of the trial in midcourse.
You can assess the type I error rate from simulated trials where the parameters are fixed at the borderline values for which the device should not be approved. The proportions of successful trials in these simulations provide an estimate of the maximum type I error rate. FDA recommends that several likely scenarios be simulated and that the expected sample size and estimated type I error be provided in each case.
You can assess power (and the type II error rate) from simulated trials where the parameters are fixed at plausible values for which the device should be approved. The proportions of unsuccessful trials in these simulations provide estimates of the type II error rate. The complement estimates the power provided by the experimental design. FDA recommends several likely scenarios be simulated and that the expected sample size and estimated type II error rate and power be provided in each case.
If FDA considers the type I error rate of a Bayesian experimental design to be too large, we recommend you modify the design or the model to reduce that rate. Determination of “too large” is specific to a submission because some sources of type I error inflation (e.g., large amounts of valid prior information) may be more acceptable than others (e.g., inappropriate choice of studies for construction of the prior, inappropriate statistical model, or inappropriate criteria for study success). The seriousness (cost) of a Type I error is also a consideration.
There are many options for decreasing the type I error rate. These options include:
- increasing the posterior (or predictive) probability that defines a successful trial (e.g., 97 percent, 98 percent, 99 percent),
- increasing the number of patients before the first interim analysis,
- reducing the number of interim analyses,
- discounting the prior information,
- Choice of hyperprior parameter values
- Discounting historical data
- Limiting the effective number of patients “borrowed” from the historical control
- Including an inflation factor on the variance between studies in hierarchical models
- Putting restrictions on the amount of borrowing that is allowed from previous studies14
- increasing the maximum sample size (again, to reduce the influence of the prior),
- changing the criteria for terminating enrollment in an adaptive trial,
- Altering the calculation of type I error rate, or
- Inclusion (or not) of prior information in the calculation of type I error
- Inclusion (or not) of covariate adjustments in the calculation of type I error
- Calculation of type I error at appropriate point(s) away from the null boundary. Clinical judgment will help define “appropriate.”
- Calculation of “average” type I error integrating over the prior distribution, conditional on the null.
- any combination of the above options
In case the experimental design is modified, we recommend you carry out a new set of simulations to evaluate the new design.
We may also ask you to characterize the sensitivity of the operating characteristics to assumptions made about the trial (e.g., various model and distributional assumptions and, with Bayesian trials, the choice of prior, and, for adaptive trials, rate of accrual, etc.).
7.3 Model Selection
Some statistical analysis plans allow for comparison of several possible models of the data and parameters before a final model is chosen for analysis. For example, in a Bayesian analysis of a study outcome that borrows strength from other studies, the effects of a factor on the outcome might vary from study to study. Two possible models that you may want to consider might be (1) a model in which the factor effects do not vary by study and (2) a more expansive model in which they do.
One method of comparing two models tests the null hypothesis that one model is true against the alternative that the other model is true. The result of such a test depends on the posterior probability of the alternative model, or the posterior odds for the alternative model. Posterior odds refer to the ratio of the posterior probability of the alternative model to the posterior probability of the null model. According to Bernardo and Smith (1994), an optimal decision for choosing the true model among a finite set of possible models for a given data set is to choose the model with highest posterior probability. Thus, posterior odds is often a preferred method of model comparison.
Prior odds, on the other hand, refer to the ratio of the prior probability of the alternative model to the prior probability of the null model. For a given alternative model, the ratio of posterior odds to prior odds is referred to as the Bayes Factor. Thus, a Bayes Factor is said to represent the change in odds of an alternative model over a null model, say, as we move from prior to posterior. Thus the Bayes Factor could potentially be used for model selection. By comparing the posterior odds to the prior odds, the Bayes factor may be robust to the choice of prior distribution. We should note, however, that Bayes Factors are not well-defined for some non-informative priors, specifically when the prior distribution is improper (does not integrate to one). Carlin and Louis (2008) offer more details on Bayes Factors and their computation.
In addition, Bayesian deviance measures such as Deviance Information Criterion (DIC, Spiegelhalter et al., 2002) can be used for model choice by comparing the fit of one model over another. DIC appears as an option in the WinBUGS program. It is calculated as the posterior mean of the model deviance minus the effective number of parameters in the model (pD) where the effective number of parameters is the decrease in deviance expected from estimating the parameters of the model. pD can be estimated as the posterior mean of the deviance minus the deviance evaluated at the posterior mean of the parameters (Gelman et al., 2003, p. 182, give a good discussion of effective number of parameters). The model with the minimum DIC provides the best fit to the data.
7.4 Checking Exchangeability using the Posterior Predictive Distribution
In Section 5.5, we discuss using the predictive distribution to check certain assumptions of the model used to fit to the data. In this section we describe how one might use predictive distribution to assess exchangeability of the current study and several historical studies. Exchangeability is determined from a clinical and engineering standpoint at the planning stage. However, sometimes we can also check this assumption statistically.
Suppose an adverse event rate was observed to be much higher in a new study than in historical studies, despite a clinical judgment of exchangeability of studies prior to collecting data on the new study. To simplify discussion, suppose no covariates are available that could account for the difference. Then, we might use posterior predictive analysis to check whether the difference is unlikely under the exchangeable model being considered in the prior distribution. One possible test statistic is the smallest absolute difference between the observed rate for the new study and another study rate, a type of gap statistic. If this observed gap is large compared with similarly defined gaps between the historical studies, then the new and historical study rates may not be exchangeable. This observed gap statistic can be compared with its posterior predictive distribution, calculated under the exchangeable model. The exchangeable model is not supported if the observed gap is located far into the right-hand tail of its posterior predictive distribution. A summary is to compute the posterior predictive probability of observing a gap at least as large as that observed, which is called the Bayesian p-value for the gap. If the Bayesian p value is small, then the exchangeable model may not hold. A more technical discussion is given in Pennello and Thompson (2008) .
7.5 Calculations
Almost all quantities of interest in a Bayesian analysis involve the calculation of a mathematical integral. All the following are expressed as an integral involving the posterior distribution:
- the posterior mean,
- the posterior standard deviation,
- the credible interval, and
- the posterior probability of a hypothesis.
The following are some numerical integration techniques used to compute these integrals:
- Gaussian quadrature,
- posterior distribution sampling,
- Laplace approximation,
- importance sampling, and
- Markov Chain Monte Carlo (MCMC) techniques (Gamerman and Lopes 2006).
MCMC techniques are probably the most commonly used; the most used MCMC technique is the Gibbs sampler. The Metropolis-Hastings algorithm is a generalization that can be used in cases where the Gibbs sampler fails.
MCMC techniques are popular because in many analyses, the posterior distribution is too complex to write down, and therefore traditional numerical integration techniques like quadrature and Laplace approximation cannot be carried out. The Gibbs sampler draws samples from other, known distributions to create a (Markov) chain of values. A Markov chain is a set of samples where the value at each point depends only on the immediately preceding sample. Eventually, as the chain converges, the values sampled begin to resemble draws from the posterior distribution. The draws from the Markov chain can then be used to approximate the posterior distribution and compute the integrals.
Tanner (1996) provides a survey of computational techniques used in statistics, including numerical integration and MCMC techniques. Gilks et al. (1996) explains MCMC techniques and their application to a variety of scientific problems. Discussion of MCMC and other techniques also appear in Gamerman and Lopes (2006), Gelman et al. (2004), and many other textbooks.
When MCMC techniques are used, FDA recommends you check that the chain of values generated has indeed converged at some point so that subsequent draws are from the posterior distribution. Various techniques have been developed to diagnose nonconvergence. You may refer to diagnostic techniques discussed in Gelman et al. (2004), Gilks et al. (1996), Tanner (1996), Gamerman and Lopes (2006), and the manual for CODA (Convergence Diagnosis and Output Analysis), a set of SPlus functions that process the output from the program BUGS (Bayesian inference using Gibbs sampling).15
Convergence difficulties
Depending on how the Bayesian model is parameterized, the Markov chain might converge very slowly. Alternative parameterizations or alternative MCMC samplers may help to speed up convergence. One possible explanation for a chain that does not seem to converge is that an improper prior distribution was used (see Section 5: Analyzing a Bayesian Clinical Trial). In that case, the chain may not converge because a proper posterior distribution does not exist. When improper prior distributions are used, you should check that the posterior distribution is proper. Convergence difficulties can also occur when the prior distribution is nearly improper.
Data augmentation
The technique of data augmentation introduces auxiliary variables into a model to facilitate computation. The use of auxiliary variables can also aid in the interpretation of your analysis. For example, latent variables are now commonly introduced in analyses of ordinal outcomes (i.e., outcomes with only a few possible values that are ordered). Examples of such outcomes include answers to multiple-choice questions for a quality of life questionnaire. Johnson & Albert (1999) discuss Bayesian analysis of ordinal outcomes using latent variables. Tanner (1996) discusses data augmentation as a general technique.
Electronic submission of calculations
For Bayesian or other analyses that entail intensive computation, FDA will routinely check the calculations (e.g. for convergence of the Markov chain when using MCMC techniques). We recommend you submit data and any programs used for calculations to FDA electronically.
8. References
Albert (2007) Bayesian Computation with R Springer.
Barlow, R. E., Irony, T. Z., & Shor, S. W. W. (1989). Informative sampling methods: The influence of experimental design on decision, in influence diagrams, beliefs nets and decision analysis. Oliver and Smith (Eds.), John Wiley & Sons.
Berger, J. O. (1986) Statistical Decision Theory and Bayesian Analysis, Springer.
Berger, J. O. & Berry, D. A. (1988). The relevance of stopping rules in statistical inference. Statistics decision theory and related topics, IV 1. S. S. Gupta and J. O. Berger (Eds.). Berlin: Springer, 29–72 (with discussion).
Berger, J. O., & Wolpert, R. L. (1988). The likelihood principle, Second Ed. CA: Hayward: IMS.
Bernardo & Smith. (1993). Bayesian theory, John Wiley & Sons.
Berry, D. A. (1996). Statistics, a Bayesian perspective. Duxbury Press.
Berry, D. A. (1997). Using a Bayesian approach in medical device development. Technical report available from Division of Biostatistics, Center for Devices and Radiological Health, FDA.
Berry, D. A., & Stangl, D. K. (Eds). (1996). Bayesian biostatistics. New York: Marcel Dekker.
Berry, D. A. (1988), Multiple Comparisons, Multiple Tests, and Data Dredging: A Bayesian Perspective, In Bayesian Statistics 3, Bernardo, DeGroot, Lindley, Smith (Eds), pp. 79-94.
B land, J. M., & Altman, D. G. (1998). Bayesians and frequentists. BMJ, 317(24), 1151.
Box, G. E. P. (1980) Sampling and Bayes’ inference in scientific modeling and robustness. . Journal of the Royal Statistical Society, Series A, 143, 383–430.
Box, G. E. P., & Tiao, G. C. (1973). Bayesian inference in statistical analysis. MA: Reading: Addison Wesley.
Breslow, N. (1990). Biostatistics and Bayes. Stat Sci 5(3), 269–284.
Broemeling, L. D. (2007) Bayesian Biostatistics and Diagnostic Medicine, Chapman & Hall.
Brophy, J. M., & Joseph, L. (1995). Placing trials in context using Bayesian analysis: GUSTO, revisited by Reverend Bayes. JAMA, 273, 871–875.
Carlin, B.P., and Louis, T. (2008) Bayesian methods for Data Analysis, 3 rd ed.. Chapman and Hall.
Carlin, B. P., Kadane, J. B., & Gelfand, A. E. (1998). Approaches for optimal sequential decision analysis in clinical trials. Biometrics, 54, 964–975.
Chen, M. H., & Shao, Q. M. (1999). Monte Carlo estimation of Bayesian credible and HPD intervals. Journal of Computation and Graphical Statistics, Vol. 8, N.1, 69–92.
Congdon, P. (2003). Applied Bayesian modeling, Wiley.
Congdon, P. (2007) Bayesian Statistical Modelling 2 nd edition
Congdon, P. (2005) Bayesian Models for Categorical Data, Wiley.
DeGroot, M. H. (1970) Optimal Statistical Decisions, McGraw-Hill.
De Groot, M. H. (1986). Probability and statistics, Addison Wesley.
Dey, D., Muller, P., & Sinha, D. (Eds.) (1998). Practical nonparametric and semiparameteric Bayesian statistics. New York: Springer-Verlag.
Dixon, D. O, Simon R. (1991). Bayesian subset analysis. Biometrics 47, 871–882 .
DuMouchel, W. (1999). Bayesian data mining in large frequency tables, with an application to the FDA spontaneous reporting system. American Statistician, 53 (3), 177–202.
Duncan, D. B. and Dixon, D. O. (1983), k-ratio t tests, t intervals and point estimates for multiple comparisons. In Encyclopedia of Statistical Sciences, Vol. 4, Kotz and Johnson (eds). New York:Wiley)
Gamerman, D. and Lopes, H. F. (2006). Markiv chain Monte Carlo: Stochastic simulation for Bayesian inference, second edition. Chapman & Hall.
Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. (2004). Bayesian data analysis . Second Ed., London: Chapman and Hall.
Gelman, A., Meng, X., & Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica, 6, 733–760, discussion 760–807.
Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. (1996). Markov chain monte carlo in practice . London: Chapman & Hall.
Gonen, M., Westfall, P. H., and Johnson, W. O. (2003), Bayesian Multiple Testing for Two-Sample Multivariate Endpoints, Biometrics, 59, 76–82.
Goodman, S. (1999a). Toward evidence-based medical statistics, 1: the p value fallacy. Annals of Internal Medicine, 130, 995–1004.
Goodman, S. (1999b). Toward evidence-based medical statistics, 2: the Bayes factor. Annals of Internal Medicine, 130, 1005–1013.
Gould, A. L. (1991). Using prior findings to augment active-controlled trials and trials with small placebo groups. Drug Information Journal, 25, 369–380.
Hively, W. (1996, May). The mathematics of making up your mind. Discover, 90–97.
Ibrahim, J. G., & Chen, M. H. (2000). Power distributions for regression models. Statistical Science, 46–60.
Inoue, L. Y. T., Berry, D.A., & Parmigiani, G. (2005). Relationship between Bayesian and frequentist sample size determination. The American Statistician, 59, 79–87.
Irony, T. Z. (1992). Bayesian estimation for discrete distributions. Journal of Applied Statistics, 19, 533–549.
Irony, T. Z. (1993). Information in Sampling Rules. Journal of Statistical Planning and Inference,36, 27–38.
Irony, T. Z., & Pennello, G. A. (2001). Choosing an appropriate prior for Bayesian medical device trials in the regulatory setting. In American Statistical Association 2001 Proceedings of the Biopharmaceutical Section. VA: Alexandria: American Statistical Association.
Irony, T. Z, & Simon, R. (2006).“Application of Bayesian Methods to Medical Device Trials”, in Clinical Evaluation of Medical Devices, Principles and Case Studies, Becker, K. and Whyte, J., 2 nd Edition.
Irony, T. Z. (2007). “Evolving Methods: Evaluating Medical Device Interventions in a Rapid State of Flux” in the proceedings of the Institute of Medicine roundtable on Evidence-Based Medicine called “The Learning Healthcare System.”
Johnson, V. E., and Albert, J. H. (1999). Ordinal data modeling. New York: Springer-Verlag.
Joseph, L., Wolfson, D. B., & Berger, R., du. (1995a). Sample size calculations for binomial proportions via highest posterior density intervals. The Statistician: Journal of the Institute of Statisticians, 44, 143 – 154
Joseph, L., Wolfson, D. B., & Berger, R., du. (1995b). Some comments on Bayesian sample size determination. The Statistician: Journal of the Institute of Statisticians, 44, 167–171
Kadane, J. B. (1995). Prime time for Bayes. Controlled Clinical Trials, 16, 313–318.
Kadane, J. B. (1996). Bayesian methods and ethics in a clinical trial design. John Wiley & Sons.
Kass, R. E., & Wasserman, L. (1996). The selection of prior distributions by formal rules. Journal of American Statistical Association, 91 (435), 1343–1370.
Katsis, A., & Toman, B. (1999). Bayesian sample size calculations for binomial experiments. Journal of Statistical Planning and Inference, 81, 349–362
Lee, P. M. (1997). Bayesian statistics: an introduction. New York: John Wiley & Sons.
Lewis, R. J., & Wears, R. L. (1993). An introduction to the Bayesian analysis of clinical trials. Ann. Emerg. Med., 22(8), 1328–1336.
Lewis, C. and Thayer, D. T. (2004). A loss function related to the FDR for random effects multiple comparisons. Journal Stat Plan Inf 125, 49–58.
Lilford, R. J., & Braunholtz, D. (1996). The statistical basis of public policy: A paradigm shift is overdue. BMJ, 313, 603–607.
Lindley, D. V. (1985). Making decisions. John Wiley & Sons.
Lindley, D. V. (1997). The choice of sample size. The Statistician, 46, N. 2, 129–138.
Malakoff, D. (1999, Nov 19). Bayes offers a “new” way to make sense of numbers. Science, 286, 1460–1464.
O’Malley AJ, Normand S-LT (2003). Statistics: Keeping pace with the medical technology revolution. Chance, 16(4): 41-44.
O’Malley AJ, Normand S-LT, Kuntz RE (2003). Application of models for multivariate mixed outcomes to medical device trials: Coronary artery stenting. Statistics in Medicine, 22(2):313-336.
Pennello, G. (1997), The k-ratio multiple comparisons Bayes rule for the balanced two-way design, JASA, 92, 675-684.
Pennello, G. and Thompson, L. (2008) Experience with reviewing Bayesian medical device trials, J Biopharmaceutical Statistics, 18:1, 81-115).
Raiffa and Schlaifer (2000) Applied Statistical Decision Theory, Wiley, originally published in 1961
Robert, C. P. (2007) The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, Springer.
Rubin, D. B. (1984). Bayesianly justifiable and relevant frequency calculations for the applied statistician. The Annals of Statistics 12(4), 1151-1172.
Rubin, D. B., & S tern, H. S. (1998). Sample size determination using posterior predictive distributions. Sankhyā, Series B, 60, 161 – 175
Scott, J. G. and Berger, J. O. (2006) An exploration of aspects of Bayesian multiple testing, Journal of Statistical Planning and Inference, 136, 2144 – 2162.
Simon, R. (1999). Bayesian design and analysis of active control clinical trials. Biometrics, 55, 484–487.
Spiegelhalter, D. J., Abrams, K. R., & Myles, J. P. (2004). Bayesian approaches to clinical trials and health-care evaluation . New York: Wiley.
Spiegelhalter, D. J., Best, N. G., Carlin, B. P. and van der Linde, A. (2002)
Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society, Series B, 64, 583-616
Spiegelhalter, D. J., Freedman, L. S., and Parmar, M. K. B. (1994). Bayesian approaches to randomized trials. Journal of the Royal Statistical Society, Series A, 157, 356–416.
Spiegelhalter, D. J., Myles, J. P., Jones, D. R., & Abrams, K. R. (2000). Bayesian method in health technology assessment: A review. Health Technology Assessment, 4, 38.
Spiegelhalter, D. J., Thomas, A., Best, N. G., & Gilks, W. R. (1996). BUGS : Bayesian inference using Gibbs sampling, version 0.5 (version ii). MRC Biostatistics Unit. Retrieved February, 2002, from http://www.mrc-bsu.cam.ac.uk.
Stangl, D.K., & Berry, D.A. (Eds.) (1998). Bayesian statistics in medicine: Where are we and where should we be going? Sankhya Ser B, 60, 176–195.
Stern, H. S. (1998). A primer on the Bayesian approach to statistical inference. Stats, 23, 3–9.
Tanner, M.A. (1996). Tools for statistical inference. New York: Springer-Verlag.
1 Two examples of successful use of Bayesian methods in device trials are:
TRANSCAN (http://www.accessdata.fda.gov/scripts/cdrh/ cfdocs/cfTopic/pma/pma.cfm?num=p970033). Prior information was used to incorporate results from previous studies, resulting in a reduced sample size for demonstration of effectiveness.
INTERFIX (http://www.accessdata.fda.gov/scripts/cdrh/ cfdocs/cfTopic/pma/pma.cfm?num=p970015). An interim analysis was performed; based on Bayesian predictive modeling of the future success rate, the trial was stopped early. No prior information was used.
2 The FFDCA provides for two types of early collaboration meetings: agreement meetings and determination meetings. See §§ 513(a)(3)(D), 520(g)(7). For details, see the FDA Guidance on early collaboration meetings at http://www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/ GuidanceDocuments/ucm073604.htm .
3 However, one example can be seen at INTERFIX labeling at (SSE: http://www.accessdata.fda.gov/scripts/cdrh/cfdocs /cfTopic/pma/pma.cfm?num=p970015).
4 The WinBUGS program can be downloaded from the website of the Medical Research Center, Cambridge: www.mrc-bsu.cam.ac.uk. OpenBUGS can be found at http://mathstat.helsinki.fi/openbugs/
6 http://www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/ GuidanceDocuments/ucm106757.htm
7 See 21 CFR 812.20(b)(2) and 21 CFR 812.27.
8 http://www.accessdata.fda.gov/scripts/cdrh/ cfdocs/cfTopic/pma/pma.cfm?num=p980048.
9 http://www.accessdata.fda.gov/scripts/cdrh/ cfdocs/cfTopic/pma/pma.cfm?num=P000058.
10 http://www.accessdata.fda.gov/scripts/cdrh/ cfdocs/cfTopic/pma/pma.cfm?num=p980048.
11 See Summary of Safety and Effectiveness for PMA P970015 at http://www.accessdata.fda.gov/scripts/cdrh/cfdocs/ cfTopic/pma/pma.cfm?num=p970015.
12 See the Summary of Safety and Effectiveness for PMA P970015 at http://www.accessdata.fda.gov/scripts/cdrh/cfdocs/ cfTopic/pma/pma.cfm?num=p970015).
13 See http://www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/ HowtoMarketYourDevice/PremarketSubmissions/ucm136377.htm for information on submitting clinical data in electronic form.
14 In a regulatory setting, it is of paramount concern if the result of current study is substantially different from that of previous studies. Therefore, a restriction on the amount of borrowing might be determined at the design stage according to relevant experts’ input. For example, to guide against using the previous control data when the serious adverse event rate of the current control arm is substantially smaller than that of the previous study, an empirical rule may be set such that if the serious adverse event rate of the current control arm is smaller than that of the previous study by a fixed number, no data from the previous study will be used. Such empirical rules should be reflected in simulations of the operating characteristics.
15 Both programs may be downloaded from the Medical Research Center, Cambridge, at http://www.mrc-bsu.cam.ac.uk
Submit Comments
Submit comments on this guidance document electronically via docket ID: FDA-2013-S-0610 - Specific Electronic Submissions Intended For FDA's Dockets Management Staff (i.e., Citizen Petitions, Draft Proposed Guidance Documents, Variances, and other administrative record submissions)
If unable to submit comments online, please mail written comments to:
Dockets Management
Food and Drug Administration
5630 Fishers Lane, Rm 1061
Rockville, MD 20852
All comments should be identified with the title of the guidance.